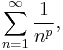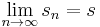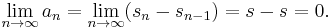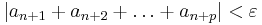Term test
In mathematics, the nth term test for divergence[1] is a simple test for the divergence of an infinite series:
- If
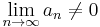 or if the limit does not exist, then
or if the limit does not exist, then 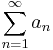 diverges.
diverges.
Many authors do not name this test or give it a shorter name.[2]
Contents |
Usage
Unlike stronger convergence tests, the term test cannot prove by itself that a series converges. In particular, the converse to the test is not true; instead all one can say is:
- If
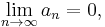 then
then 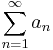 may or may not converge. In other words, if
may or may not converge. In other words, if 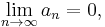 , the test is inconclusive.
, the test is inconclusive.
The harmonic series is a classic example of a divergent series whose terms limit to zero.[3] The more general class of p-series,
exemplifies the possible results of the test:
- If p ≤ 0, then the term test identifies the series as divergent.
- If 0 < p ≤ 1, then the term test is inconclusive, but the series is divergent by the integral test for convergence.
- If 1 < p, then the term test is inconclusive, but the series is convergent, again by the integral test for convergence.
Proofs
The test is typically proved in contrapositive form:
- If
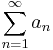 converges, then
converges, then 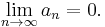
Limit manipulation
If sn are the partial sums of the series, then the assumption that the series converges means that
for some number s. Then[4]
Cauchy's criterion
The assumption that the series converges means that it passes Cauchy's convergence test: for every 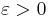 there is a number N such that
there is a number N such that
holds for all n > N and p ≥ 1. Setting p = 1 recovers the definition of the statement[5]
Scope
The simplest version of the term test applies to infinite series of real numbers. The above two proofs, by invoking the Cauchy criterion or the linearity of the limit, also work in any other normed vector space.[6]
Notes
- ^ Kaczor p.336
- ^ For example, Rudin (p.60) states only the contrapositive form and does not name it. Brabenec (p.156) calls it just the nth term test. Stewart (p.709) calls it the Test for Divergence.
- ^ Rudin p.60
- ^ Brabenec p.156; Stewart p.709
- ^ Rudin (pp.59-60) uses this proof idea, starting with a different statement of Cauchy criterion.
- ^ Hansen p.55; Șuhubi p.375
References
- Brabenec, Robert (2005). Resources for the study of real analysis. MAA. ISBN 0883857375.
- Hansen, Vagn Lundsgaard (2006). Functional Analysis: Entering Hilbert Space. World Scientific. ISBN 9812565639.
- Kaczor, Wiesława and Maria Nowak (2003). Problems in Mathematical Analysis. American Mathematical Society. ISBN 0821820508.
- Rudin, Walter (1976) [1953]. Principles of mathematical analysis (3e ed.). McGraw-Hill. ISBN 0-07-054235-X.
- Stewart, James (1999). Calculus: Early transcendentals (4e ed.). Brooks/Cole. ISBN 0-534-36298-2.
- Șuhubi, Erdoğan S. (2003). Functional Analysis. Springer. ISBN 1402016166.